Latest News
April 22, 2021 - CSAT Quiz
1. P works thrice as fast as Q, whereas P and Q together can work four times as fast as R. If P, Q and R together work on a job, in what ratio should they share the earnings?
(a) 3 : 1 : 1
(b) 3 : 2 : 4
(c) 4 : 3 : 4
(d) 3 : 1 : 4
Solution:
P : Q = 3 : 1
(P + Q) : R = 4 : 1 = (3 + 1) : 1
P : Q : R = 3 : 1 : 1
(a) 3 : 1 : 1
[Note: If A can work x times faster than B, then A’s share of work shall be x/(x+1)th part of the total work]
2. Consider the following relationships among members of a family of six persons A, B, C, D, E and F:
Hence the answer is option (c):
(c) 12
5. How many of the three-digit numbers are divisible by 7?
(a) 108
(b) 116
(c) 124
(d) 128
Solution:
Arithmetic Progression
Find the total number of terms in an arithmetic sequence
By using the formula
n = [(L- a)/d] + 1
we can find the total number of terms of an arithmetic sequence.
L - Last term
a = first term
d = common difference (a2 - a1)
Example
How many terms are there in the following Arithmetic progressions ?
-1,-5/6,-2/3,……………10/3
Solution :
First term (a) = -1
Common difference (d) = a2 – a1
d = (-5/6) – (-1)
d = 1/6
n = [(L-a)/d] + 1
L = 10/3
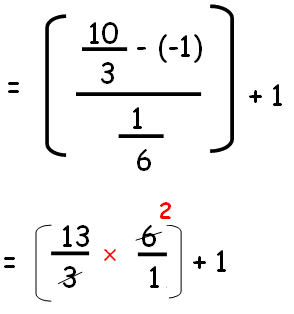n = 27
Hence, 27 terms are in the given A.P
The minimum three digit number divisible by 7 is 105 and maximum number is 994.
Hence, a=105,d=7,L=994
L=a+(n-1)d;
994=105+(n-1)7
by solving,we get
n=128.
[OR]
The number of multiples of x in the range= ( [Last multiple of x in the range − First multiple of x in the range] / x )
+1
Last 3-digit multiple of 7 is 994;
First 3-digit multiple of 7 is 105;
So the number of 3-digt multiples of 7 is [(994−105)7]+1=128
(d) 128
- The number of males equals that of females.
- A and E are sons of F.
- D is the mother of two, one boy and one girl.
- B is the son of A.
- There is only one married couple in the family at present.
Hence the answer is option (c):
(c) 12
5. How many of the three-digit numbers are divisible by 7?
(a) 108
(b) 116
(c) 124
(d) 128
Solution:
Arithmetic Progression
Find the total number of terms in an arithmetic sequence
By using the formula
n = [(L- a)/d] + 1
we can find the total number of terms of an arithmetic sequence.
L - Last term
a = first term
d = common difference (a2 - a1)
Example
How many terms are there in the following Arithmetic progressions ?
-1,-5/6,-2/3,……………10/3
Solution :
First term (a) = -1
Common difference (d) = a2 – a1
d = (-5/6) – (-1)
d = 1/6
n = [(L-a)/d] + 1
L = 10/3
n = 27
Hence, 27 terms are in the given A.P
The minimum three digit number divisible by 7 is 105 and maximum number is 994.
Hence, a=105,d=7,L=994
L=a+(n-1)d;
994=105+(n-1)7
by solving,we get
n=128.
[OR]
The number of multiples of x in the range= ( [Last multiple of x in the range − First multiple of x in the range] / x )
+1
Last 3-digit multiple of 7 is 994;
First 3-digit multiple of 7 is 105;
So the number of 3-digt multiples of 7 is [(994−105)7]+1=128
(d) 128
POSTED ON 22-04-2021 BY ADMIN
Next previous 
General Studies
Political Science and International Relations
Some Reference Essays
List of previous year essay topics (1997-2019)
IAS GOOGLE is googled by the team of Raja Sir’s Cracking IAS Academy. Sources include The Hindu, Indian Express, pib.nic.in, Down To Earth, Economic Times, Vigyan Prasar, AIR and the like. IAS GOOGLE has been prepared in pace with emerging UPSC Trends.